天才数学者の知性のきらめき、絵や音楽などの背景にある芸術性、AIとビッグデータをサポート使いやすさ…あまりにも美しく、あまりにも深いととても便利な学問的な数学の魅力を、身近な話題を導入語りかける文章、丁寧な説明で解明数学エッセイ “巨大な数学「この6月4日に発刊。発売4日で1万部の大増刷後も再版が続いている。
鎌田浩毅氏（京都大学教授） “数学 “ゼロ”を持っている私トラウマを解消してくれた「（「プレジデント2020/9/4号」） “人気のある数学塾院長が、数学の深さと美しさ、社会への影響力などを数学愛いっぱいつづる。読みやすく編集されて、数学の扉が開かれるきっかけになるかもしれない「（朝日新聞2020/7/25掲載）、佐藤優さん」長野博之の「驚異的な数学」は粉飾会計を見抜く力をつけるためにも有効である「（「週刊ダイヤモンド2020/7/18号」）、教育界YouTuberよビノリ巧さん “様々な角度から「数学の美しさ」を実感することができる一冊！」と歓声ている。 2020年ノーベル物理学賞に英国オックスフォード大学のロジャー・ペンローズ氏が選ばれた。 優れた数学者でもあるペンローズ氏の受賞を祝う著者が緊急寄稿した。連載のバックナンバーは、ここで。
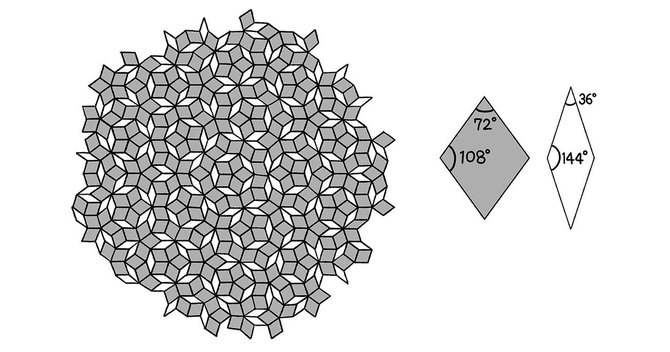
【ペンローズのタイル】イラスト：小さな鳥デスコ[펜로즈타일】일러스트:작은새들데스코
2種類のダイヤモンドで平面を埋め尽くす
数学の三大分野と言えば、方程式を扱う「代数」関数を扱う「解釈学」、そして図形を扱う「幾何学」の3つのことをいう。
幾何学的に紀元前1000年頃から研究が始まり、今も活発な議論が行われている分野がある。 タイリングやテッセレーションと呼ばれるもので、日本語では平面充填（重点）する。
距離の報道と建築物などに見られるタイルの様々な模様があり、すべての非常に美しい。 いわゆる「だまし絵」の第一人者である、オランダの画家・版画家のマウスリッツコルネリスエッシャー（1898〜1972）も瓦」無限に続くパターン “に魅せられた一人だ。 エッシャーが40代以降のユニークな敷かれて形を描くようになったのは、スペインのアルハンブラ宮殿から見た素晴らしいタイル装飾に感化されたためだった。
しかし、タイルの使用図形は何でもいいわけではない。 無限に続く平面状のタイルで埋め尽くそうとしたときどのような形であれば、隙間と重複しないように敷かれてできるかどうかを考えている」平面充填問題」は、とても奥が深いものである。
しばらく前に、2020年ノーベル物理学賞に選出された英国のロジャー・ペンローズ（1931〜）は、優れた物理学エーザイエーザイ平面充填問題を言うときには欠かせない数学でもある。
ペンローズ理論物理学者、スティーブン・ホーキング（1942〜2018）と一緒にブラックホール」特異整理」を研究した。 そして一般相対性理論で重力が無限大になる」特異点」、すなわちブラックホールが存在するということを証明し、これが今回のノーベル賞の主な受賞理由となった。
ペンローズは、いわゆる「不可能物体 “の研究でも知られている。”ペンローズの三角形」とか「ペンローズの階段」という絵を見たことがあるか。
その不可能物体は表示できる立体の平面図で見えますが、よく見ると、このような物体は、現実にはありえないことがわかる（例えば、「ペンローズの階段」は、階段を上ってしまったところが階段の下部に接続されている）と呼ばれる奇妙な図ある。
人間の感覚や物事の現実について一石を投入不可能物体は、今では数学だけでなく、哲学者や心理学者、そして美術家などにも注目を集めており、広い分野に影響を及ぼしている。
よりペンローズは1972年に「ペンローズのタイル」を考案「平面充填問題」も大きな足跡を残した。 ペンローズのタイルは、2種類のダイヤモンドを持っている法則に基づいてソートして平面を埋めたものをいう。 特筆すべきは、その行が定期的ではないという点である。 ペンローズのタイルの部分をどのように平行移動してもぴったり重ならず、他の部分が存在する。
ペンローズのタイルに代表されるような定期ませ平面充填商品のほとんどは、主に20世紀に入ってから発見された。 それまで平面充填といえば長方形を使用したタイルのように “の形全体を平行移動すると、重なる」という特徴を持つものがほとんどであった。非周期的平面充填方法を考案するためには、まれなインスピレーションに加えて、高度な近現代数学が必要である。
数学を指導したという事実は、思わぬ形で応用されることができる。 ペンローズのタイルもその例に漏れない。
1982年にイスラエルの化学者ダニエルシューヒート万（1941〜）は、周期的な構造を持たない合金を発見した。 それまでに決定すると、周期的な構造を持つことが「常識」だったので、発表当時シューヒートマンは激しい批判を受けることになる。
しかし、彼はペンローズのタイルを理論的に裏付けすることにより、非周期的な構造を有する結晶であること（準結晶という）も存在得る断固主張した。 以後「準結晶」が続々と発見されたもので、シューヒートだけの成果は認められ、2011年にノーベル化学賞を受賞している。
ペンローズの幾何学の功績は、人の形の鋭い洞察力を与えるだけでなく、遊び心と数学の膨大な可能性を物語っている。 そんな氏のノーベル賞受賞を心からお祝いしたい。
（本稿は、 “巨大な数学“に掲載された内容に大幅な加筆を加えたものです）
+ There are no comments
Add yours