Subaru HSCデータの中からEASを効果的に取得するには、さまざまなデータ収集条件でSubaru HSC画像にトラックを残すと予想されるランダムな方向のバックグラウンド電磁粒子とミューオニック粒子の数のモデルを定式化する必要があります。 私達はこの値にラベルを付けます \(N_{\textrm{モデル}}\)。 様々な貢献 \(N_{\textrm{モデル}}\) 望遠鏡の仰角、望遠鏡の方位角、空の明るさのレベルを以下に説明します。 \(\psi _{\textrm{電話}}\)、 \(\phi _{\textrm{電話}}\)そして \(B_{\textrm{空}}\) それぞれ。 方位角ゼロ度は南に定義され、方位角は時計回りに増加した。
有効面積
検出されたトラックの数は、CCDの有効検出領域に比例すると予想されます。 この面積自体は、望遠鏡が指す方向と入ってくる宇宙船方向との間の角度分離余弦の絶対値に比例する。 宇宙船の方位角を考慮すると、 \(\phi _{\textrm{CR}}\)そして宇宙船天頂閣、 \(\theta _{\textrm{CR}}\)角度分離の余弦は次のように指定されます。
$$\begin{ソート} \cos \alpha = \cos \theta _{\textrm{CR}} \sin \psi _{\textrm{tel}} + \sin \theta _{\textrm{CR}} \ cos \psi _{\textrm{tel}} \cos (\phi _{\textrm{tel}}-\phi _{\textrm{CR}}) \end{aligned}$$
(1)
どこ \(\アルファ\) 角度の分離です。
地球における宇宙船フラックスの天頂角依存性を次のように仮定すると \(\cos ^{2} \theta _{\textrm{CR}}\)望遠鏡高度で予想される宇宙船 \(\psi _{\textrm{電話}}\) 立体角積分に比例します
$$\begin{aligned} \int _{0}^{2\pi } \int _{0}^{\pi /2} \cos ^2 \theta _{\textrm{CR}} ~ | \cos \アルファ| ~ \sin \theta _{\textrm{CR}} ~ d\theta _{\textrm{CR}} ~ d\phi _{\textrm{CR}} = \frac{\pi }{4}(1+ \sin ^2\psi _{\textrm{tel}})。 \end{ソート}$$
(2)
したがって、用語 \((1+\sin ^2 \psi _{\textrm{tel}})/2\) 私たちのモデルでは、1/2の正規化係数が選択され、項が1になるように選択されました。 \(\psi _{\text {tel}} = 90^{\circ }\) (西)。
東西効果
東西効果は、地球の磁場によって東から到着する低エネルギー量の宇宙船が抑制される現象です。14、15,16。 方位角の定義を使用すると、この効果は項に比例してモデル化できます。 \(\sin (\phi _{\textrm{tel}})\)。
夜空の背景
私たちは夜空の背景を定義し、 \(B_{\textrm{空}}\)は、露光期間中のCCDアレイ全体のADCカウントの中央値です。 この値は、バックグラウンドフォトンフラックスによって変化します。 経験的に、我々はより高い値があることを観察した。 \(B_{\textrm{空}}\) 一般に、より多くのトラックが検出される。 これらの追加のトラックは、実際の二次粒子ではなくトラック検出アルゴリズムの「偽」トリガーと見なされます。 正確な依存性のため \(B_{\textrm{空}}\) 検出されたトラック数が不明であるため、モデルは基本的な線形関係を想定しています。
上記の効果を追加すると \(N_{\textrm{モデル}}\) ~である
$$\begin{ソート} N_{\textrm{モデル}} = c_0 + c_1 (1+\sin ^2(\psi _{\textrm{tel}}))/2 + c_2\sin (\phi _{ \textrm{tel}}) + c_3 B_{\textrm{sky}} \end{aligned}$$
(サム)
どこ \(c_0\)、 \(c_1\)、 \(c_2\) そして \(c_3\) パラメータが適しています。 ここでは、 \(c_0\) 使用されるさまざまなフィルタのさまざまな応答を説明するためのオフセットを表します。
これらのパラメータを見つけるために、2014年3月から2020年1月の間にSubaru HSCによって収集されたデータに上記の関数を適用しました。 Subaruは、特定のフィルタと露光時間を使用して空を測定したものを「訪問」としてマークします。 この研究では、露光時間が150秒または200秒の訪問を使用しました。 下表1は、フィルタ別測定期間、期間別訪問回数、1回訪問露出時間、該当総露出時間(小計)を示すデータをまとめたものである。 すべてのフィルタをまとめて約875時間のデータが提供されました。
訪問ごとに専用のソフトウェアを使用して、長い直線、ワーム状、またはくさび状のトラックなどのさまざまな形状を検索して、画像内のトラック数を計算しました。 トラックは一連の条件に基づいて識別され、主にローカル背景のピクセル強度と画像内の天体の点拡散機能のグラデーションチェックを考慮しました。 手順はセクション 4.4 で詳しく説明されています。17。 二次粒子によって汚染されていると疑われるピクセルは、隣接するイベントにグループ化され、繰り返しプロセス中にさらに綿密に調査されました。
各訪問のトラック数を計算すると、夜空の背景レベルとともに望遠鏡の高度と方位角を抽出した。 次に、式3を次の方法を使用して各フィルタのデータに合わせました。 当初、モデルはEASを含むイベントを含むすべてのデータに適していました。 \(\値 ^2\) そうだね目標は数をモデリングすることだったから 背景トラック その後、モデル予測とは異なる複数のトラックを持つデータポイントを削除しました。 \(2\シグマ\)どこ \(\シグマ\) 測定データと適合モデルとの間の平均二乗誤差の標準偏差でした。 次に、式3を残りのデータに戻し、最適なパラメータを記録しました。 図 2 にデータとモデル継手の例を示します。
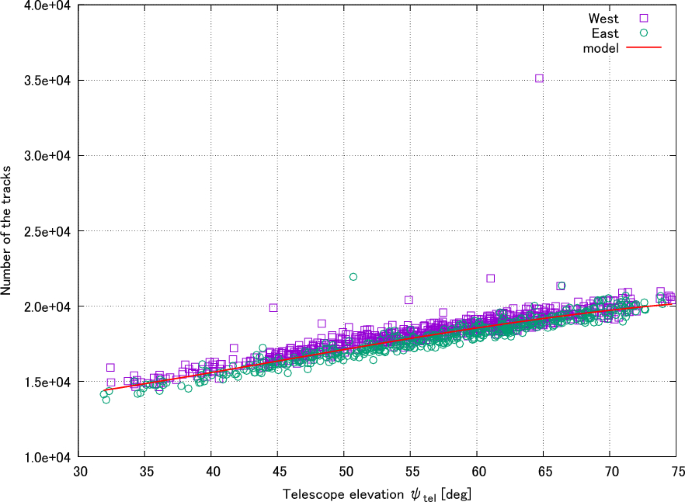
Eq. 継手の単純化された例。 3 さまざまな訪問回数を追跡します。 横軸は望遠鏡の仰角を表す。 縦軸は、訪問時に検出されたトラック数を示します。 紫色の四角形と緑色の円は、それぞれ西と東を指す望遠鏡で撮影したデータを表します。 主なイベントグループの上にはいくつかのポイントがあります。 これらのポイントはEASである可能性が高く、2を適用すると削除されます。\(\シグマ\) しきい値(テキストを参照)。 赤い線はモデル適合結果を示しています。 \(\phi _{\textrm{tel}} = 0^{\circ }\) そして \(B_{\textrm{空}} = 1000\) 重要です。
すべてのフィルタのパラメータ化結果を表2に示します。 \(\シグマ\)。
仰角への依存性(\(c_1\)) はすべてのフィルタでほぼ同じです。 さらに、方位角の変化(\(c_2\))は、東西効果で予想されるように、西から来る宇宙船トラックの数が東から来るよりも多いことを示しています。 次の値 \(c_3\) の一般的な値と同じくらい比較的小さい。 \(B_{\textrm{空}}\) 1000個ほどになります。 最後に、 \(c_0\) 様々なフィルタにわたって特に同じ光学帯域を観察するにもかかわらず、HSC-rは、HSC-r2よりもバックグラウンドレベルがはるかに大きいことが分かる。 これは、B270に天然放射性同位元素であるカリウムが含まれているためです。














+ There are no comments
Add yours