[연재 : 수학 생물학의 생명관 # 5]生命システムの修復 – 現象の背後にある普遍性を目指し| academist Journal

[연재 : 수학 생물학의 생명관]
＃1の研究者や芸術家の共通点を探す
＃2花をモデルにしたグラフィック作品を制作するアーティストの観点から
＃3命を扱うアーティストが提示する「感得者を含むモデル」の可能性
＃4現状と数学的モデルの相互作用がもたらす美しさ
＃5生命システムの修復 – 現象の背後にある普遍性を目指し
＃6「モデリング」で芸術と科学を再融合

2019年9月に修理生物学会が開催したシンポジウム「数理生物学の生命観」に登壇した畠山哲央氏は、生命システムの物理学の構築を試み研究をいくつかも行なっています。

本記事は、現象の背後にある限定的な普遍性の比喩を寛容し、普遍的な性格の展開をしようとする物理的なアクセスを概要日時計とオーバーフロー代謝を事例として紹介しました。 普遍性を推定する作業は、芸術にも通じるものがあるかもしれません。

なぜ概日リズムは、すべての生き物に共通の性質を表すか

これは、実際の発想だと思いますが、現状があるときに最初にその背後にあるいくつかの普遍性があるかを考えています。 この普遍性は、必ずしも実際の一般的なものではなく、ある程度限定されたものかもしれません。 そしてたとえ（たとえ）を援用しながら普遍性を利用して、モデルを削ったの背後にある数学的構造を保持する新しい予測を実施する。 今までそうして理論を構築してきました。

まず、例として概要日時計の話をします。 生物は、様々な種類の普遍概要日時計を持っていることが知られています。 細菌、真菌、植物、パリ、人間など様々な生物で概日リズムが研究されてきた。 概日リズムは、毎日のサイクルに適応に重要なのですが、生物の種類に応じて全く異なる遺伝子を使用してクロックシステムを実現しています。 少なくとも4つの種から独立して進化してきたことが知られています。

生物の種類に応じて使用する遺伝子が違うすべての生物概日リズムは、3つの性質を示すことで知られています。 一つ目は、一定の環境下で約24時間周期のリズムを刻むこと。 第二は、周期が温度、栄養補償を示すこと。 よく教科書で化学振動の例として出てくるBZ反応（ベロ嘘後・ジャボチンスキー反応）の場合、温度を変化させると周期が半分程度です。 しかし、概日リズムの周期は、温度変化も大きく変わりません。 それにもかかわらず、外部からの温度変化を加えると概日リズムはとてもきれい同期することが知られています。 この同期することができるということが第三の特徴です。

つまり、概要日時計の周期は、温度に堅牢（注：変更するのは難しいこと）を見せ、一方で位相（注：振動現象の周期の中でどのような状態の位置時計で言えば、一つ一つの時間が一つの位相に対応する）は、温度に焼成（注：可変的なもの）を示すものです。 これは時計を作る遺伝子が異なっても普遍的な特徴であることが知られています。 このような性質は、一見相反するように見えるが、この二つの何か関係があるのか​​という疑問でした。

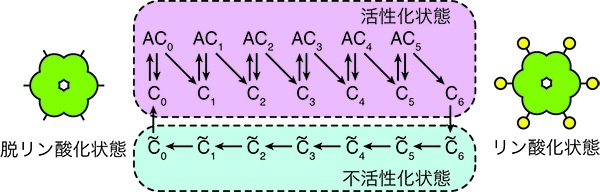
だからまずは細菌の概要日時計の数学的モデルを構築しました。 シアノバクテリアの概要日時計は非常に面白いシステムです。 周辺の時計を見せたいと思います時計は非常に多くの部分で行うことができます。 しかし、細菌の概要日時計はKaiA、KaiB、KaiCは3つの蛋白質とエネルギー源（ATP注：アデノシン三リン酸、細胞内での主要なエネルギー源）を試験管に混ぜるだけで、24時間周期の振動を示す驚きの性質を持っています。 このKaiCの最大のタンパク質がリン酸化して、脱リン酸化し、24時間周期で繰り返します。

このモデルは、基本的にすべての反応が生化学系のミハエル・リース – メンテン式に描写されています。 このモデルは、3つの蛋白質は、全量試験管の中で増えたり減ったりしていないので、記憶容量があります。 そしてKaiCがリン酸化されることで様々な他の状態を有するデー一定量のKaiAを維持形になっています。

まず、元の温度補償を示すかどうかが重要です。 調べてみると、このモデルは、適切に温度補償を示した。 それぞれの化学反応の速度が温度に対して指数関数的に付与されるため、ある程度の高温と周期は温度に指数関数的に行動します。 一方、特定の温度以下では、周期が温度にほとんど依存しないことを知ることができました。 つまり、温度が低い領域では、このモデルでは、温度補償を表します。

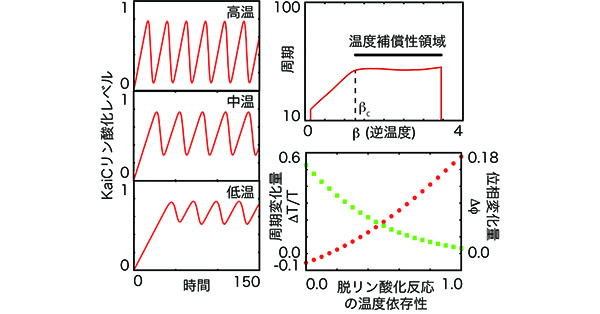
温度補償性が起こる理由直感的な説明であるが、低温になるとリン酸化の回路を回っているKaiCの実効的な量が減少してKaiCによると、KaiA争奪戦が弱くなります。 するとKaiCと結合していない自由のKaiAが増加します。 そして、その量の変化が反応速度の変化を無視し、バッファ（緩衝）で働くことを知ることができました。 それぞれの反応は、温度が低くなると遅くなりますが、無料KaiAの量がバッファに遅くなっ反応速度を補償します。

ここで私たちが今一番考えて問題というのは、温度補償を示す概要日時計が温度の位相の焼成を同時に示すことができるのはなぜかということでした。 重要なことは、この性質が非常に普遍的であるということです。

Kaiタンパク質のモデルで知り合ったという事実は、生化学反応速度は温度に依存するが、他の反応がそれを補償するバッファの役割を奪って温度補償を示すものです。 そこサイクルの堅牢性の一般的なメカニズムがあるではないかと思われます。 環境が変化したときに、律速反応速度は当然変わります。 それを無視するようにどのような反応がバッファとして働く場合に、従って周期の変化を抑制することができるではないか。 このような構造がKaiタンパク質のモデル研究を通じて見せてきました。

比喩を援用しながらだとしたが、このバッファからの速度の変化を無視構造が何か似ないか考えるときにどのように入力のXという要素の変化を、Yの要素を同時に変化させて中和ように見えるので、フィードフォワード（注：制御方法の一つ。システム生物学の研究では、実際の生物の遺伝子制御ネットワークのフィードフォワードよく利用されているのが発見されたし）による適応ネットワークと表示されています。

だからサイクルの堅牢性は、リミットサイクル（注：巻かスプリングからエネルギーを受けてリズムをメトロノームのように、外部からのエネルギーを受けて生じる振動する。すべての生き物のリズムは限界サイクルと見なすこと）の後での適応現象に把握されているではないかは、予測をしました。

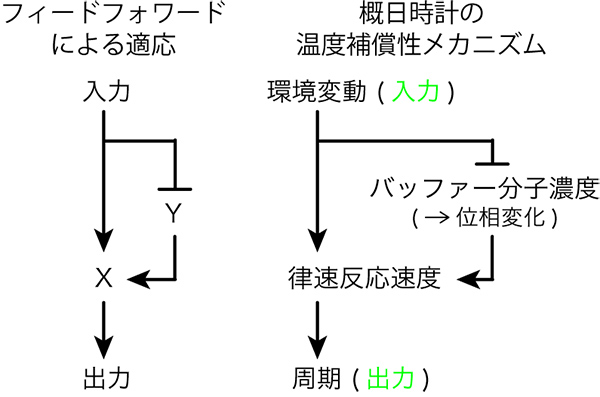
もしこの適応は十分強ければ周期の変化は小さくなるが一方で、過渡的にバッファの量が変化するので、位相が大きく異なります。 つまり、適応が十分強ければ周期の変化は小さくなり、位相の変化が大きくなることが予想されます。 一方、適応が弱ければ周期の変化が大きくなり、位相が少しずつ変更されることが予想されます。 つまり、サイクルの堅牢性と位相の焼成は、普遍的に両立することが予想されます。

実際見てみると、Kaiタンパク質のモデルは、周期の温度補償を表す場合、一時的に温度を変化させると、位相がより大きく変わりました。 これ実際の生物の中で時計の状態です。 一方、温度変化に周期が大きく異なる位相がほぼ変わらないことがわかりました。

ここまではKaiタンパク質の話でしたが、先ほどの構造は非常に普遍的に行われるものと予想されました。 だから九州大学のゲン佐庸さんと理研の黒澤前さんが昔していたショウジョウバエの概要日時計モデルも見てみました。 ショウジョウバエの概要日時計はKaiタンパク質とは全く異なる構造で振動をしていますが、それにもかかわらず、見事サイクルの堅牢性と位相の焼成の間の関係が成立しました。 他にも様々な時計の例では、この関係は非常に普遍的であることを知っていました。

いくつかの現象を理解しようとするとき、その中に隠れている普遍性を考えて、例えを援用しながら、その本質的な構造を探すにはアクセスは、高速日時計の例は、非常に有効であったとするでしょう。

オーバーフロー大使とミクロ経済学のアナロジー

2番目の例は、オーバーフロー代謝です。 呼吸は非常に効率的にATPを生成することができる代謝経路です。 しかし、増殖中の細胞は、ATP生成の効率に落ちる代謝経路である発酵が酸素の存在下でも使用されていることが知られています。 これオーバーフロー代謝です。 これは大腸菌や酵母、がん細胞などで普遍的に見ることができることがわかります。

このオーバーフロー代謝には、さまざまな仮説が提唱されています。 例えば、呼吸がより多くのタンパク質を使用したり、必要なタンパク質を細胞膜に挿入する呼吸はより膜面積を使用するとか、呼吸はATP代謝の効率が良いが、NADPHの代謝は、発酵がより効率的であるとの仮説です。

ここで、疑問は、様々な生物に見えるのは、様々な仮説があり、その根底に何か普遍的な構造があるではないかということです。 だからセリフをミクロ経済学の比喩を用いて分析することを考えました。

増殖中の細胞は、代謝が進化の過程でどの程度最適化されていることが、最近のフラックスバランス分析などで知っています。 実際に代謝を最適化した最適化問題を解決し、代謝状態をある程度きれいに予測することができることが知られています。

一方、ミクロ経済学では、個人や企業などの経済主体が利益を最適化することを前提とし、その最適化問題を解いています。 だからセリフの問題をこのフレームワークによく載ることはないかと思いました。 特に消費者行動の理論を使用することができていると思いました。

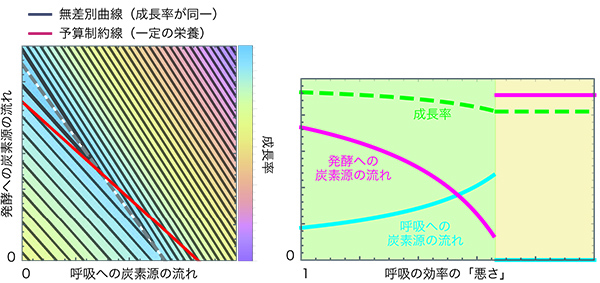
消費者行動の理論というのは、いくつかのものを一定の収入の下で消費したときに、幸福も最適化問題です。 いろいろなものを購入したときどのように幸せになるかという関数を考えて収入が一定であるとき、どのくらいの割合で購入するのが一番幸せなのかを考えています。 これオーバーフロー代謝に適用しようと思いました。

ミクロ経済学の各製品の需要が代謝では、各代謝経路の流量（フラックス）に対応しています。 予算の制約は栄養割り当てられます。 今の場合は、炭素源を呼吸に回したり、発酵石一つに対応しています。 幸福度は成長率に対応します。 これから幸せも関数を描くことができます。

このサポートを利用して、過去に提唱された様々な仮説が事実と同じ最適化問題として表現されることを知っていました。 その後、炭素源が少ないときは、ATPの効率に優れた呼吸ばかりし、炭素源が多くなっていくと、発酵をすることになる最適化の結果であると感じ正しく表示することができました。 癌細胞でも酵母でも大腸菌でも、すべての一般的な構造に支配されていることがわかりました。

また、経済学のすべての製品は、実は3種類に分類されることがわかります。 その中期ペンジェ特異商品があります。 これは、価格が上がれば、より需要が上がるという製品です。 一般的な商品は、価格が上がれば需要が下がるので、これ以上です。 驚くべきことに、オーバーフロー代謝の呼吸は、実際期ペンジェに対応していることがわかりました。 そして基ペンジェとの対応では、新しい現象を予測することができました。

たとえを通して普遍性への洞察

さて、今日は普遍性というのは、主に物理学で使用される用語であるが、例えを寛容する現象の背後にある普遍的な性格の展開をしようとする方法は、物理学に限った話ではない感じています。 生命科学は事実普遍性というのは、重要な概念であることでした。 例えば、ジャックモノは「Anything found to be true of 大腸菌 must also be true of Elephants」とし、1920年には、オランダの生化学者アルベルト・クライという人が生化学ユーティリティということを提唱しています。実際に、かつては生命科学で普遍性は、中心的な概念であったでしょうか。

美術も事実のようではないかと思います。 つまり美術でも生物の普遍性を暗に仮定しているではないかということです。 例えば、特定の種の生物に生命を代表するような作品は、多くのではないかと思います。 それとも観客に命をテーマにした作品を提示している段階で、観客の間に成立する生命観の普遍性を暗黙的に想定している場合が多いと思います。

は、アクセスがもし近かった芸術と科学はどのような違いがあるでしょう？ 私は、科学哲学者ではないので、科学的には、このようなものであるということがありませんが、科学の場合は、科学的な制約があるので、既に知っているところでは、一度に離れて行くことができません。 比喩を使用すると、若干のジャンプが、まだ制限です。

ただし、美術の場合は、意味の科学的な制約がないため、全く別の方向からのたとえを拡張したり、あるいは科学的な制約に縛られた思いはまるで思いつかないようなところに手が伸ばせるかもしれません。 個人的には芸術家たちに科学者がすでに知っていることをアプリケーションがではなく、芸術の観点から、科学者たちはまるで思いつかない比喩を提示して、人類の生命観を広げる作品を作っていただければと思います。

参照

• 触媒濃度の自律調節による体内時計の一般的な温度補償、TS HatakeyamaとK Kaneko、PNAS、2012
• 翻訳後生化学発振器期間の恒常性、TS HatakeyamaとK Kaneko、FEBS手紙、2014
• 体内時計の期間の堅牢性と位相可塑性との間の相互性、TS HatakeyamaとK Kaneko、Physical Review Letters、2015
• 大使のミクロ経済学：Giffen行動として過剰大使、JF YamagishiとTS Hatakeyama – bioRxiv、2020

講演者プロフィール
畠山哲央
生物を理解したくて、学部で工学制御工学などをマスターは、分子細胞生物学を、博士は理論物理学を学び、現在も主に理論的な側面から生命システムについて研究しています。 より深い生き物について知りたい。

この記事を書いた人

切江意味の堀部和也

値に章オト
東京大学農学生命科学研究科博士課程在学。 主に植物フェノールタイプの形状モデリングの研究を実施しています。 生物・生命に関わる芸術と文化の歴史にも関心を持って修士課程で画家モネが描いた睡蓮園芸の歴史について調べています。

堀部和也
大阪大学大学院理学研究科博士課程。 主に大脳皮質の形態づくりについてコンピュータシミュレーションを用いた研究を行っている。 仮想生物の進化をコンピュータで再現生まれ不思議なオブジェクトの観察がルーチン。 生物・生命の理論モデルでそれらを対象とする芸術に興味を持ってハッカートンであったアーティストと一緒に制作をしている。

この著者の最近の記事